CWF: Consolidating Weak Features in High Quality Mesh Simplification

Abstract

In mesh simplification, common requirements like accuracy, triangle quality, and feature alignment are often considered as a trade-off. Existing algorithms concentrate on just one or a few specific aspects of these requirements. For example, the well-known Quadric Error Metrics (QEM) approach prioritizes accuracy and can preserve strong feature lines/points as well, but falls short in ensuring high triangle quality and may degrade weak features that are not as distinctive as strong ones. In this paper, we propose a smooth functional that simultaneously considers all of these requirements. The functional comprises a normal anisotropy term and a Centroidal Voronoi Tessellation (CVT) energy term, with the variables being a set of movable points lying on the surface. The former inherits the spirit of QEM but operates in a continuous setting, while the latter encourages even point distribution, allowing various surface metrics. We further introduce a decaying weight to automatically balance the two terms. We selected 100 CAD models from the ABC dataset, along with 21 organic models, to compare the existing mesh simplification algorithms with ours. Experimental results reveal an important observation: the introduction of a decaying weight effectively reduces the conflict between the two terms and enables the alignment of weak features. This distinctive feature sets our approach apart from most existing mesh simplification methods and demonstrates significant potential in shape understanding. Please refer to the teaser figure for illustration.

Introduction

In past research, requirements such as accuracy, triangle quality, and feature alignment were often considered trade-offs. Existing algorithms, including Quadric Error Metrics (QEM) and Centroidal Voronoi Tessellation (CVT), focus on a few specific aspects but struggle to achieve a good balance. For instance, QEM, the most popular approach for mesh simplification, i nvolves a sequence of basic operations such as edge contraction. Despite its advantages in accuracy and alignment with strong features, it suffers from the degradation of weak features. In contrast, CVT focuses on maintaining an even point distribution by optimizing a set of movable points, yet it falls short in aligning with any feature lines, whether strong or weak.

In this paper, we propose a smooth functional that concurrently addresses the aforementioned requirements. This functional includes a normal anisotropy term and a CVT energy term, applied to a set of movable points on the surface. The normal anisotropy term, drawing inspiration from QEM, operates in a continuous setting, while the CVT term promotes an even distribution of points, accommodating various surface metrics. We also introduce a decaying weight to automatically balance these two terms. Optimization typically concludes within tens of iterations, with each iteration decomposing the surface into Voronoi cells. Considering that existing tools for computing Restricted Voronoi Diagrams (RVDs) cannot ensure the ``one site, one region'' property on thin-plate models, we generate an inward counterpart for each movable point and develop a simple yet effective technique to facilitate the computation of RVD on thin-plate models. We tested our functional on 100 CAD models from the ABC dataset and 21 organic models. The experimental results not only confirm that the normal anisotropy term effectively preserves accuracy and aligns strong features, while the CVT term promotes even point distribution, but they also demonstrate that the introduction of a decaying weight effectively reduces the conflict between the two terms, achieving a good balance among multiple requirements. This advantageous property makes it useful for the lightweight representation of CAD models. Additionally, it can be observed that our algorithm is particularly effective in consolidating weak features of organic shapes during mesh simplification.

Results

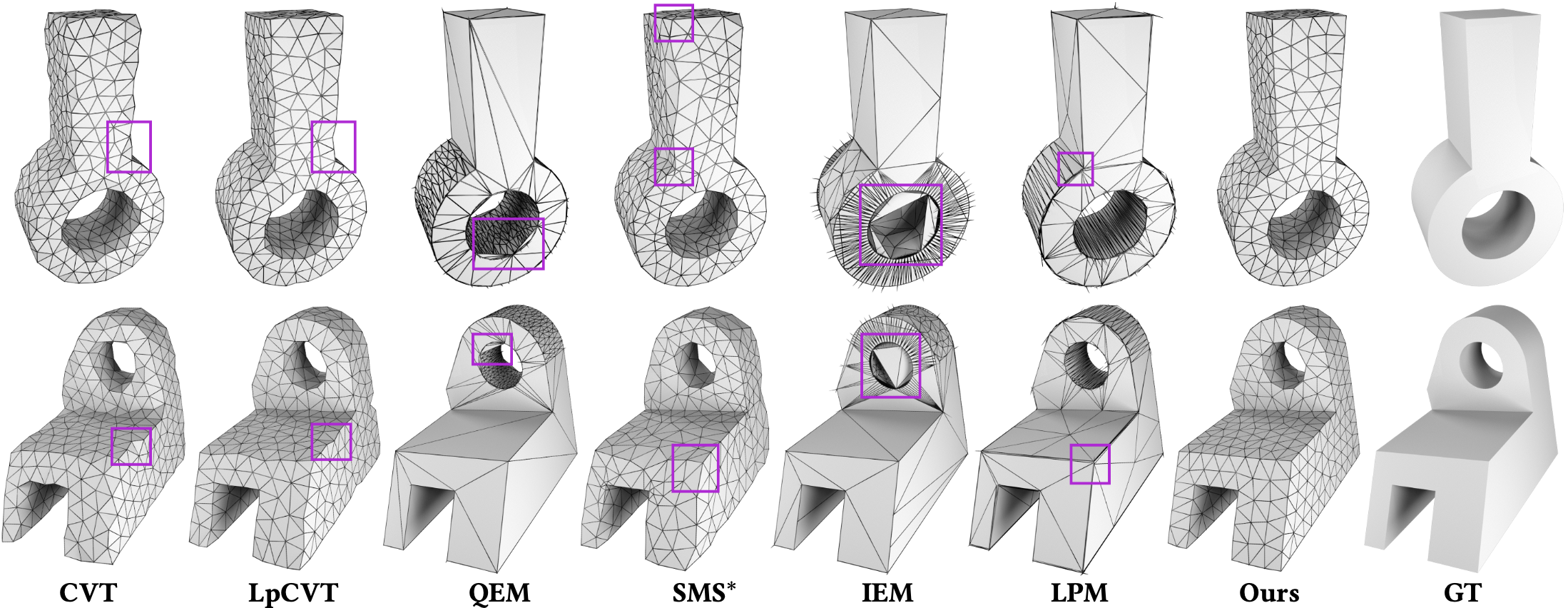
Comparison with state-of-the-art methods on two CAD inputs. Our method excels in both accuracy and manifoldness. The target number of vertices for both inputs is set at 500.

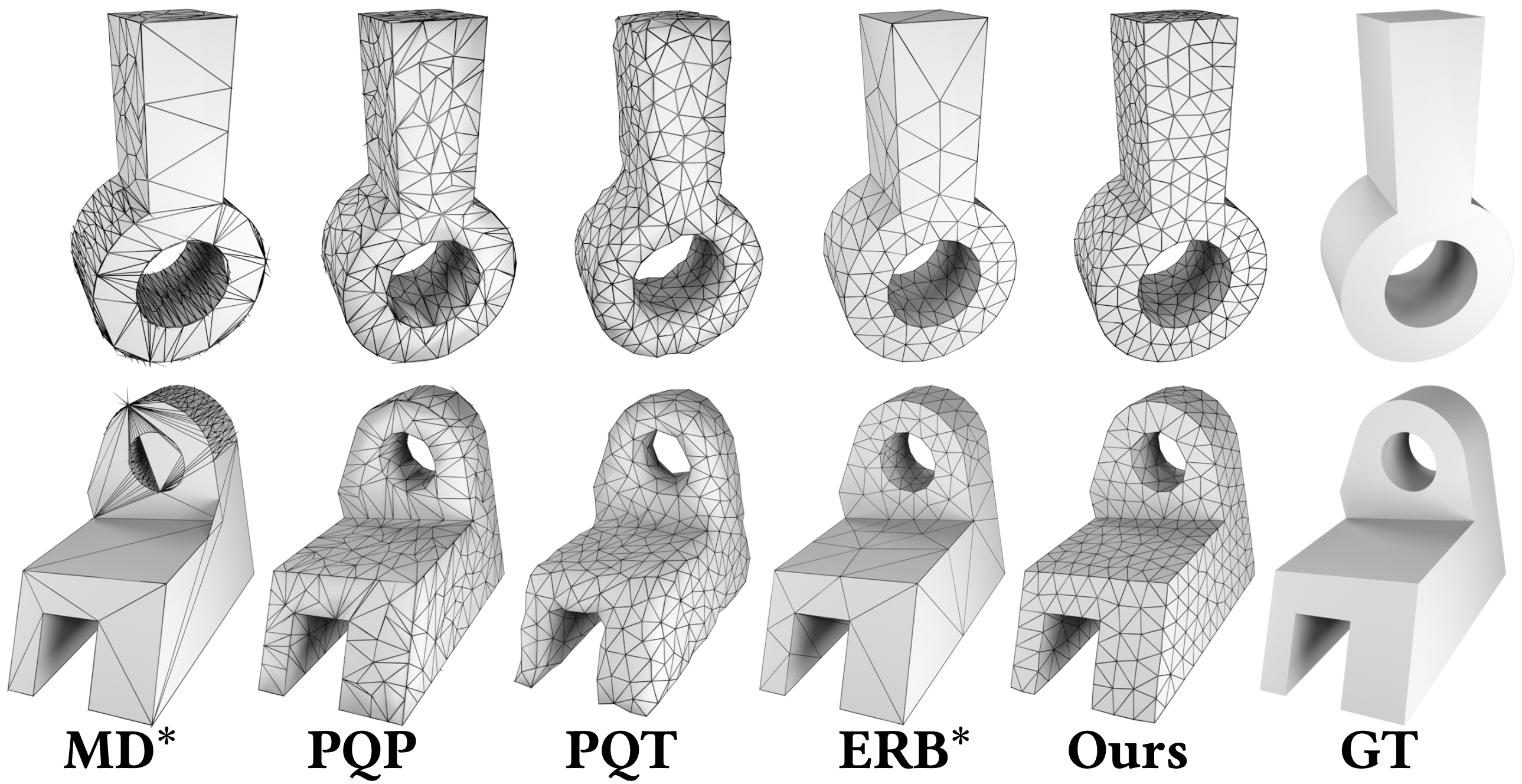
Comparison with state-of-the-art methods on two CAD inputs. The target number of vertices for both inputs is set at 500.

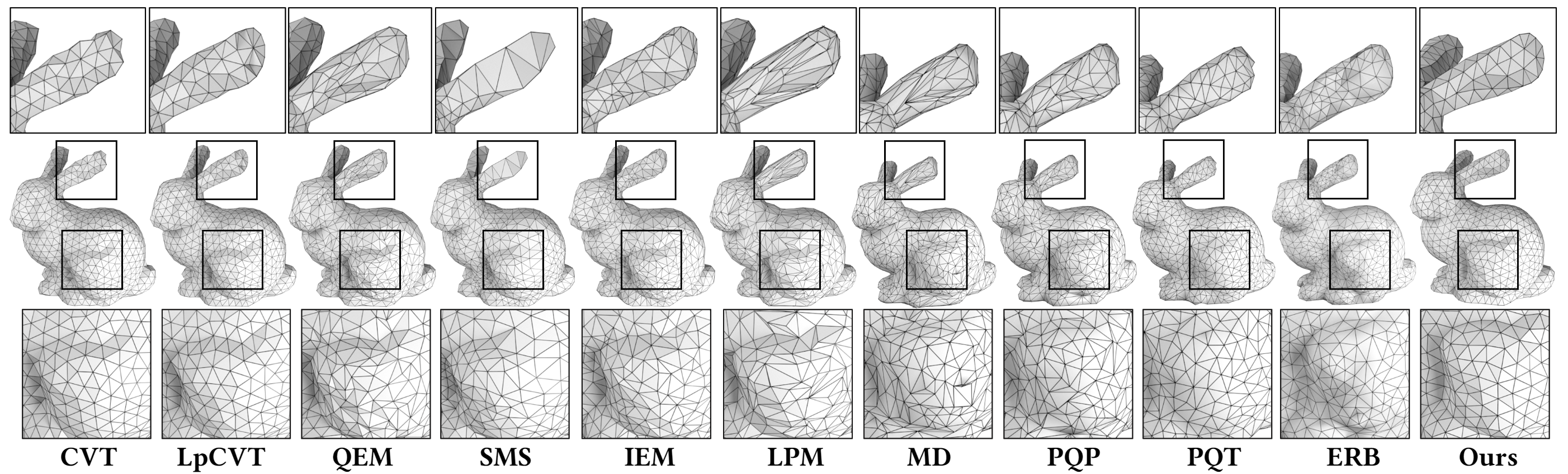
Comparison with state-of-the-art methods on the bunny model using 1000 sample points, demonstrating that our method can more effectively consolidate weak features.

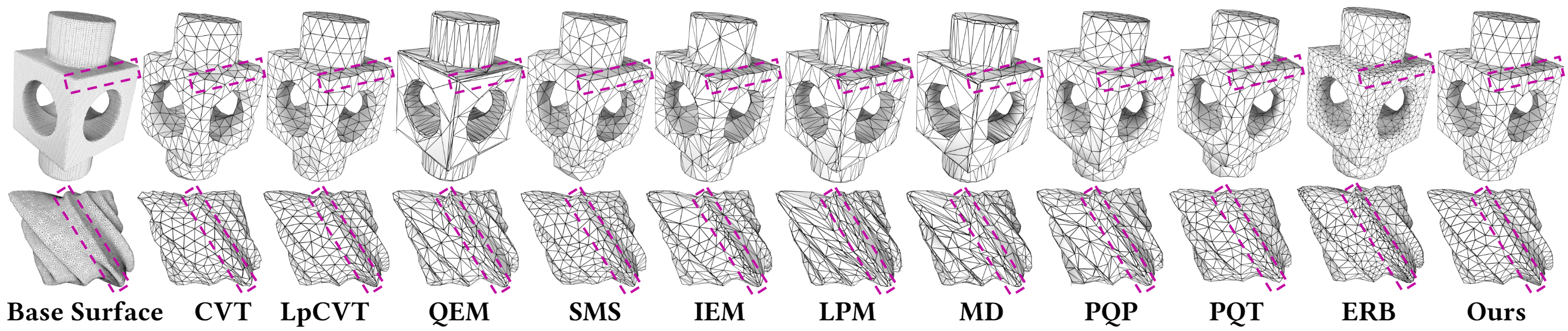
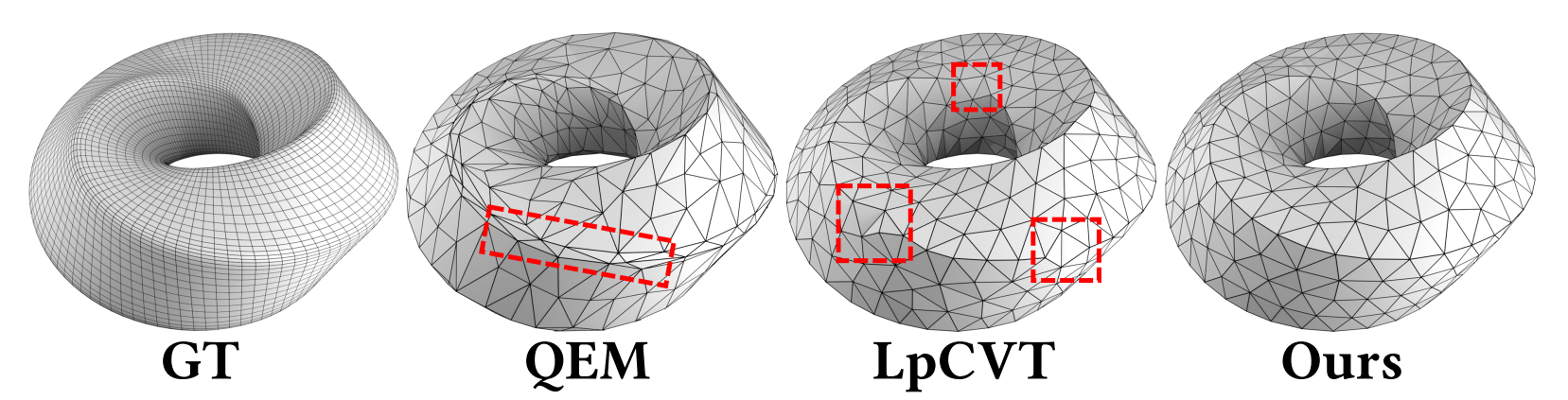
Comparison with state-of-the-art methods on two smoothed inputs. The target number of points is set at 500. Our method more effectively consolidates weak features, whereas the QEM family may result in a chamfer along the feature line.